Gumbel-Top Trick
How to vectorize sampling from a discrete distribution
If you work with libraries such as NumPy, Jax Tensorflow, or PyTorch you (should) end-up writing a lot of vectorization code: instead of using control-flow operations (e.g. for loops), you write code that operates on an entire set of values at once. Inputs and outputs of your functions are multidimensional arrays or tensors. Lower-level libraries optimized for linear algebra operations (such as matrix multiplications) make dramatic performance improvements, especially when aided by modern hardware with direct support for vector-based instructions.
In libraries like NumPy or Tensorflow sampling from a discrete distribution
without replacement is not vectorized because it requires bookkeeping. In other
words, sampling from a population depends on the values we already sampled.
So some time ago, I came across a set of re-parametrization tricks that allow us to vectorize sampling from discrete distributions. This peaked my interest because I was looking for a way to build stochastic neural networks where neuron activations could be modelled with certain types of discrete distributions parametrized by unnormalized log-probabilities.
To get a probability distribution from unconstrained vectors, usually we use the softmax function:
\[ \sigma(y) = \frac{e^{y_i}}{\sum_{j=1}^N e^{y_j}} \]
We would then use the resulting distribution to sample classes from it, for example, using the inverse transform sampling: this takes uniform samples of a number \(u\ \in [0,1)\), interpreted as a probability, and then returns the largest number \(y\) from the domain of the distribution \(P(Y)\) such that \(P(-\infty < Y < y) \le u \). What we are doing is randomly choosing a proportion of the area under the curve and returning the number in the domain such that exactly this proportion of the area occurs to the left of that number.
The Gumbel-Max Trick
The Gumbel-Max trick can be used to sample from the previous discrete distribution without marginalizing all the unnormalized log probabilities (i.e, without \(\sum_{j=1}^N e^{y_j}\)). The procedure consists in taking the unnormalized log probabilities \(y_i\), adding noise \(z_i \sim~Gumbel(0,1) \) (i.i.d. from a Gumbel distribution) and taking arg max. In other words:
\[
y = \underset{ i \in K }{\operatorname{arg max}} x_i + z_i
\]
This eliminates the need for the marginalization (which can be expensive for high-dimensional vectors). Another consequence of doing away with the computation of a normalized probability distribution, is the fact that we don’t need to see all of the data before doing partial sampling, this means Gumbel-Max can be used for weighted sampling from a stream (see this). The Gumbel Distribution is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions and, as it turns out, \(z_i\) is distributed according to a softmax function \(\sigma(y)\).
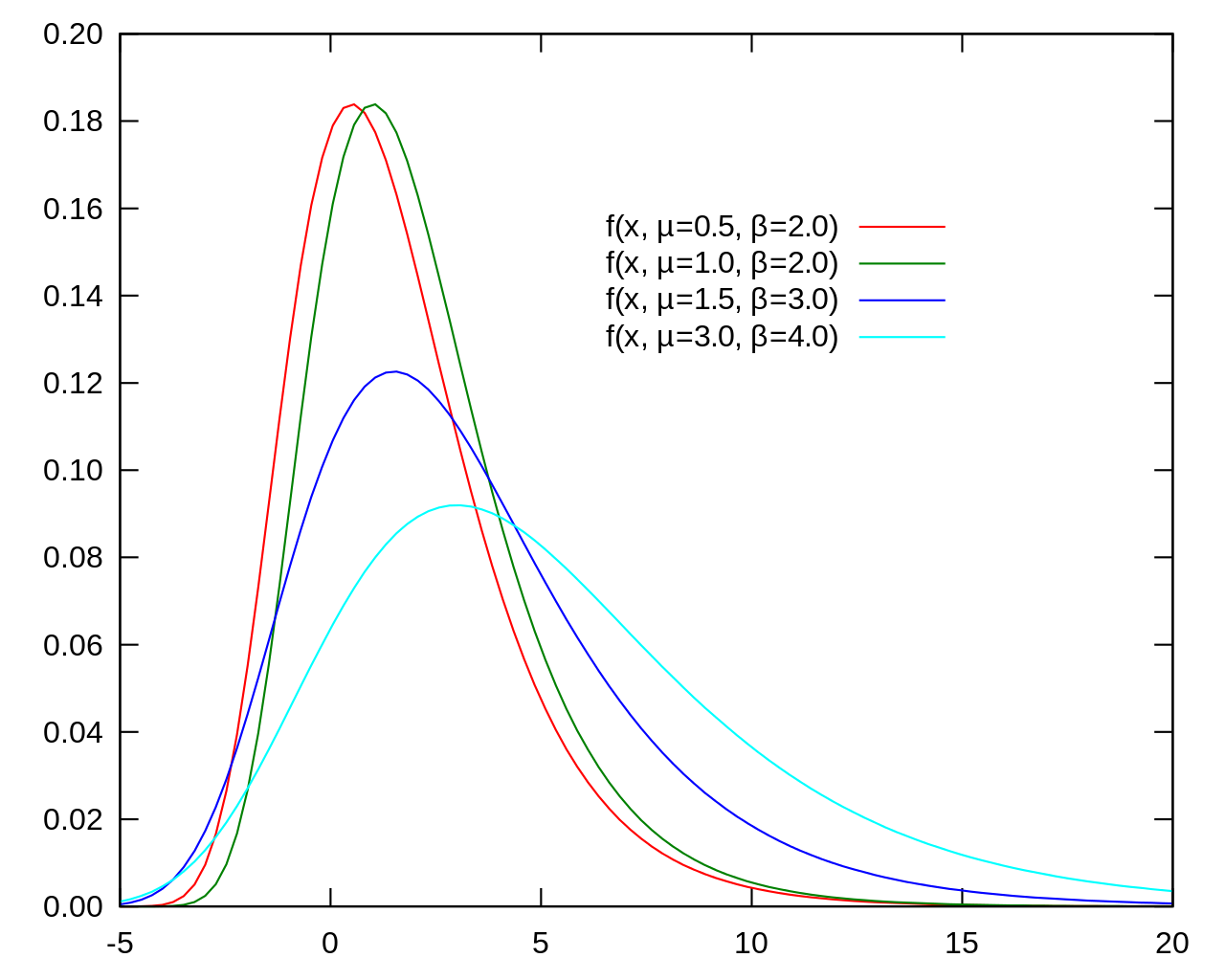
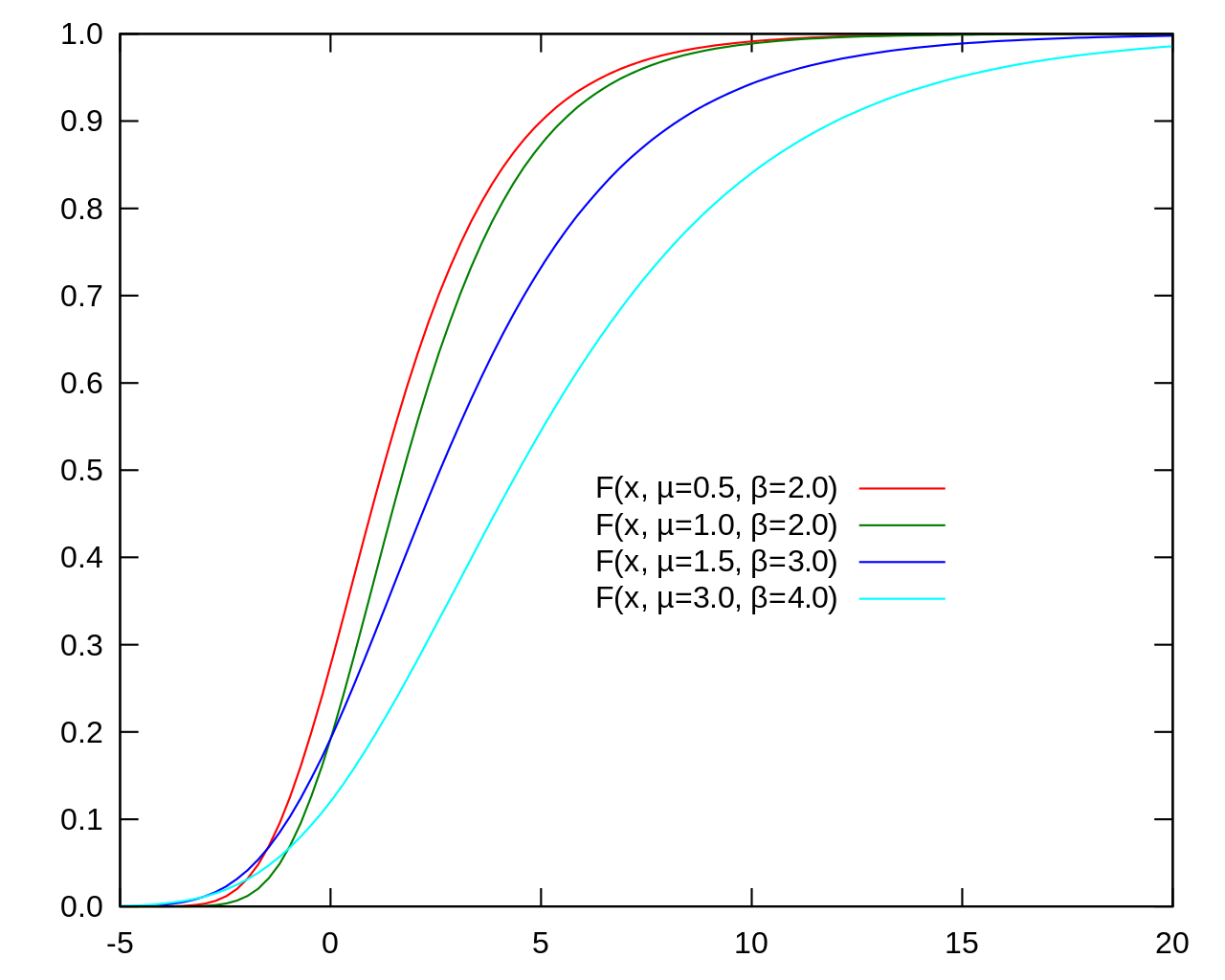
Gumbel distribution with location parameter \(\alpha\) and unit scale parameter has the following Cumulative Distribution Function (CDF):
\[ F(z;\alpha) = \exp \left[ -\exp\left[-(z-\alpha) \right]\right] \]
If \(z_k\) is the \(k^{th}\) element of the Gumbel distribution with location \(\alpha_k\), the probability that all of the other \(z_{k’\neq k}\) are less than \(z_k\) is:
\[ Pr(k > k’ | z_k, \{ \alpha_{k’}\}_{k’=1}^K) = \prod_{k’\neq k} \exp \left[ -\exp\left[-(z_k-\alpha_{k’}) \right] \right] \]
integrating the marginal distribution over \(z_k\) we have an integral which has the closed form:
\[ Pr(k > k’ | \{ \alpha_{k’}\}) = \frac{\exp\left [\alpha_k \right]}{\sum_{k’=1}^K \exp\left [\alpha_{k’} \right]} \]
which is exactly the softmax function.
The Gumbel-Top Trick
If we look at the Gumbel-Max trick as form of weighted reservoir sampling, we can see that if instead of arg max we take the top-k args, we are instead, sampling without replacement from the discrete categorical distribution. We can call this the Gumble-Top trick.
The Reparameterization Trick in Neural Networks
The reparameterization trick allows for the optimization of stochastic computation graphs via gradient descent. The essence of the trick is to refactor each stochastic node into a differentiable function of its parameters and a random variable with fixed distribution. As we have seen previously, some closed formed densities have a simple reparameterization. The choice of noise (e.g. Gumbel) gives the trick its name.
Generally speaking, this trick consists in sampling from \(p_\phi(x)\) by first sampling \(Z\) from some fixed distribution \(q(z)\) and then transforming the sample using some function \(g_\phi(z)\). This two step process is precisely what we call reparameterization trick, and it is what makes it possible to reduce the problem of estimating the gradient w.r.t. parameters of a distribution to the simpler problem of estimating the gradient w.r.t. parameters of a deterministic function. Once we reparameterized \(p_\phi(x)\), one can now express the objective as an expectation w.r.t.q(z):
\[ L(\theta, \phi)=\mathbb{E}_{X \sim p_{\phi}(x)} \left[ f_{\theta}(X) \right]=\mathbb{E}_{Z \sim q(z)} \left[ f_{\theta}\left(g_{\phi}(Z) \right) \right] \]
This trick was introduced in the context of variational inference independently by [Kingma & Welling 2014], [Rezende et al. 2014], and [Titsias & L ́azaro-Gredilla].
Implementation
Sampling from the Gumbel Distribution
We can sample \(z_i \sim \mathit{Gumbel(0,1)}\) as follows:
\[
\begin{eqnarray}
x_i \sim \mathit{Uniform(0,1)} \nonumber \\
z_i = -\log(-\log(x_i)) \nonumber
\end{eqnarray}
\]
NumPy Gumbel-Top
To finish this post and get you an idea of how simple the vectorized procedure
is, here’s an implementation using NumPy.
import numpy as np
def top_k(x, k):
return np.argpartition(x, k)[..., -k:]
def sample_k(logits, k):
u = np.random.uniform(size=np.shape(logits))
z = -np.log(-np.log(u))
return top_k(logits + z, k)
References
Blog Posts
-
Vieira, Tim. Gumbel-Max-Trick. 2014.
-
Ryans, Adam. The Gumbel-Max Trick for Discrete Distributions
-
Mena, Gonzalo. The Gumbel-Softmax Trick for Inference of Discrete Variables. 2017
Papers
-
Maddison, Chris J., Daniel Tarlow, and Tom Minka. A* sampling. Advances in Neural Information Processing Systems. 2014.
-
Kusner, Matt J., and José Miguel Hernández-Lobato. Gans for sequences of discrete elements with the gumbel-softmax distribution.
-
Jang, Eric, Shixiang Gu, and Ben Poole. Categorical reparameterization with gumbel-softmax.
-
Efraimidis, Pavlos S., and Paul G. Spirakis. Weighted random sampling with a reservoir. Information Processing Letters 97.5 (2006): 181-185.
-
Kool, Wouter, Herke Van Hoof, and Max Welling. Stochastic beams and where to find them: The gumbel-top-k trick for sampling sequences without replacement. (2019).
Comments